Published: Nov 7, 2019 by Cypherpunks Core
- 如何使用BIP-schnorr安全地為每個output節省四個權重單位
原文 : Reducing Bitcoin Transaction Sizes with x-only Pubkeys**
8 min read *By Jonas Nick
介紹 | Introduction
本文是關於最近在比特幣改進提案BIP-schnorr中引入所謂的x-only pubkeys。 BIP定義了針對比特幣的Schnorr簽名的介紹。
與現有的比特幣（ECDSA）簽名方案相比，Schnorr簽名具有提供各種好處的潛力，特別是對於典型交易而言，交易大小（和權重）更小。之所以能夠做到這一點，部分是因為Schnorr簽名支持更輕鬆地將多個簽名聚合到單個簽名中。
使用 x-only pubkeys，我們可以進一步優化，在不損失安全性的前提下，顯著降低了每個交易output的權重。
背景 | Background
通過從比特幣當前使用的壓縮public key中刪除Y坐標 byte，public key最終以32-byte表示。 我們將研究它的工作原理，為什麼有用，並概述安全性證明(security proof)。
草繪安全證明(Sketching a security proof)是一種通常可用於比特幣和閃電協議研究的技術。 它將證明丟棄的 byte不會削弱安全性，甚至不會降低”single bit”的安全性。
為了使這篇文章保持小巧美觀，我們在形式上將不做任何精確說明。 本文的主要目的是對BIP-schnorr的 x-only 部分提供基本了解。
本文假定已啟動BIP-taproot軟分叉，它定義了SegWit 在 version 1 output花費的規則。 我們不在乎新的output花費的規則是什麼，除了，新規則之一是允許使用BIP-schnorr中定義的Schnorr簽名進行消費。 需要指出的是，BIP只是建議，因此不能保證BIP-taproot會以其當前形式或完全啟動。
首先，讓我們看一下今天壓縮後的public key如何在比特幣中工作。
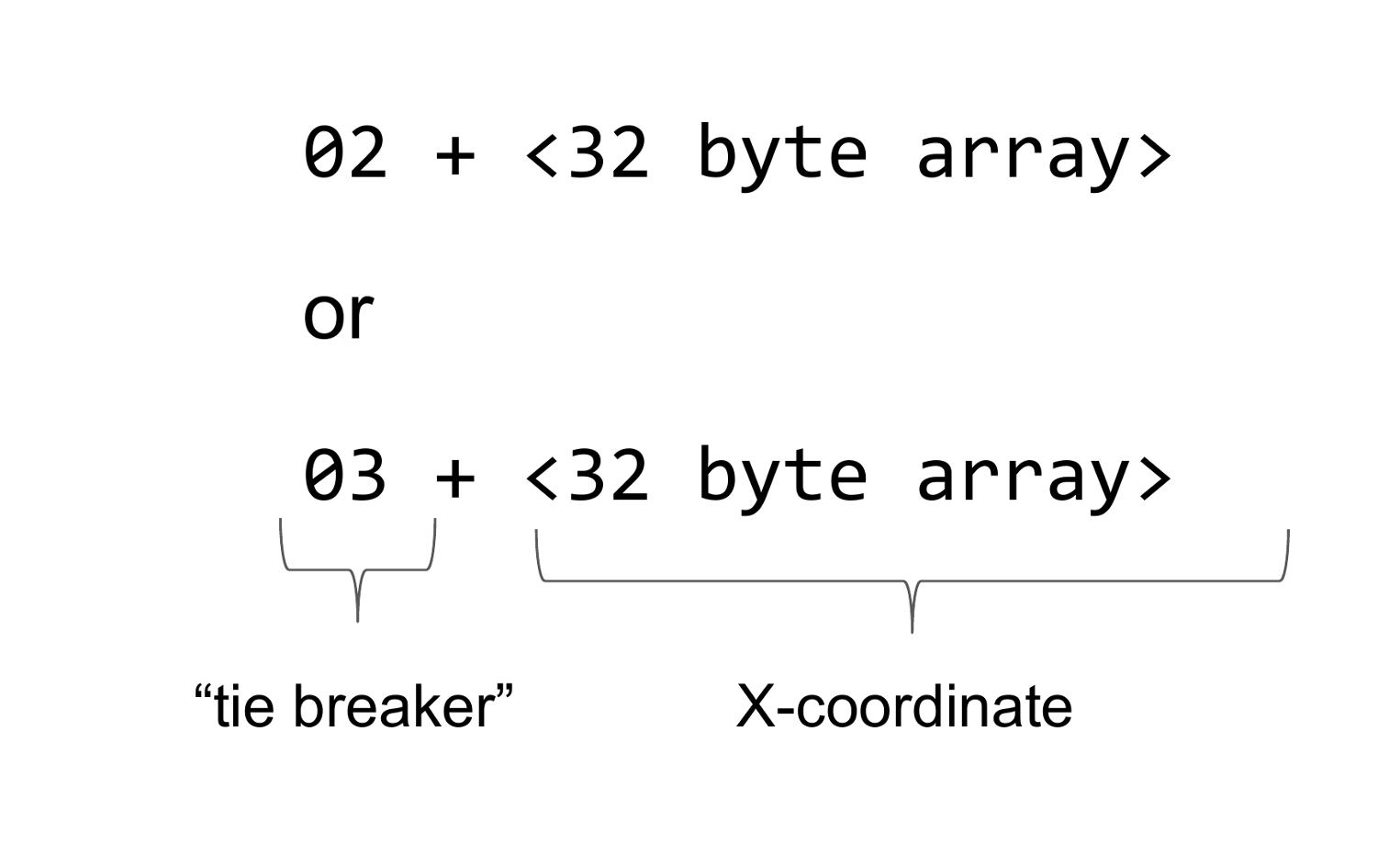
比特幣中的壓縮public key是byte 2後跟一個32 byte矩陣，或者是byte 3後跟一個 32 byte矩陣。 第一個 byte 稱為tie breaker(決勝局)，第二個部分為橢圓曲線上基礎點的X坐標。
Tie breaker的目的是什麼？
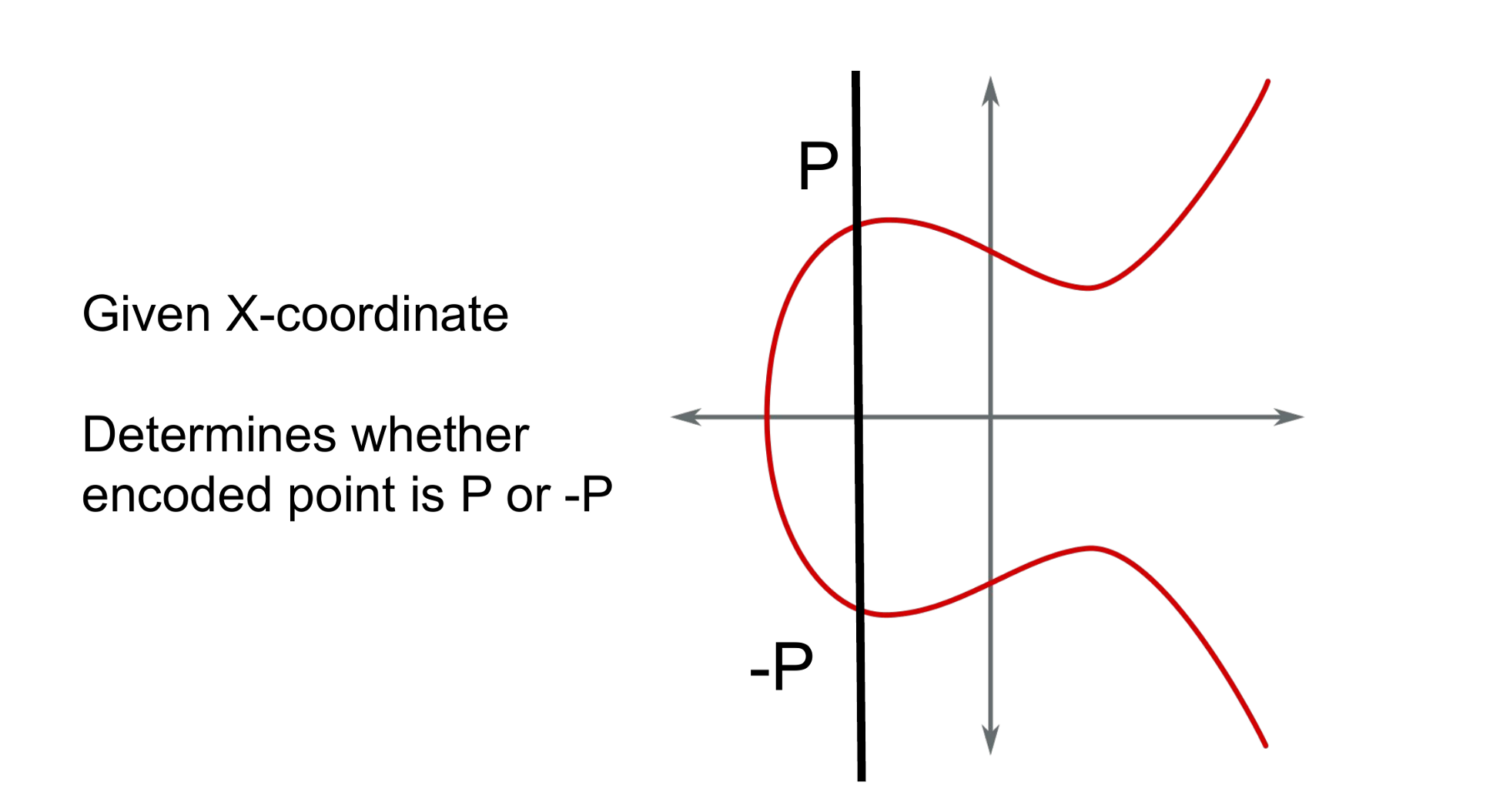
public key在橢圓曲線上編碼一個點。 僅給出X坐標，曲線上就存在兩個點。 tie breaker的目的是確定兩個點中的哪一個被編碼為P or -P。
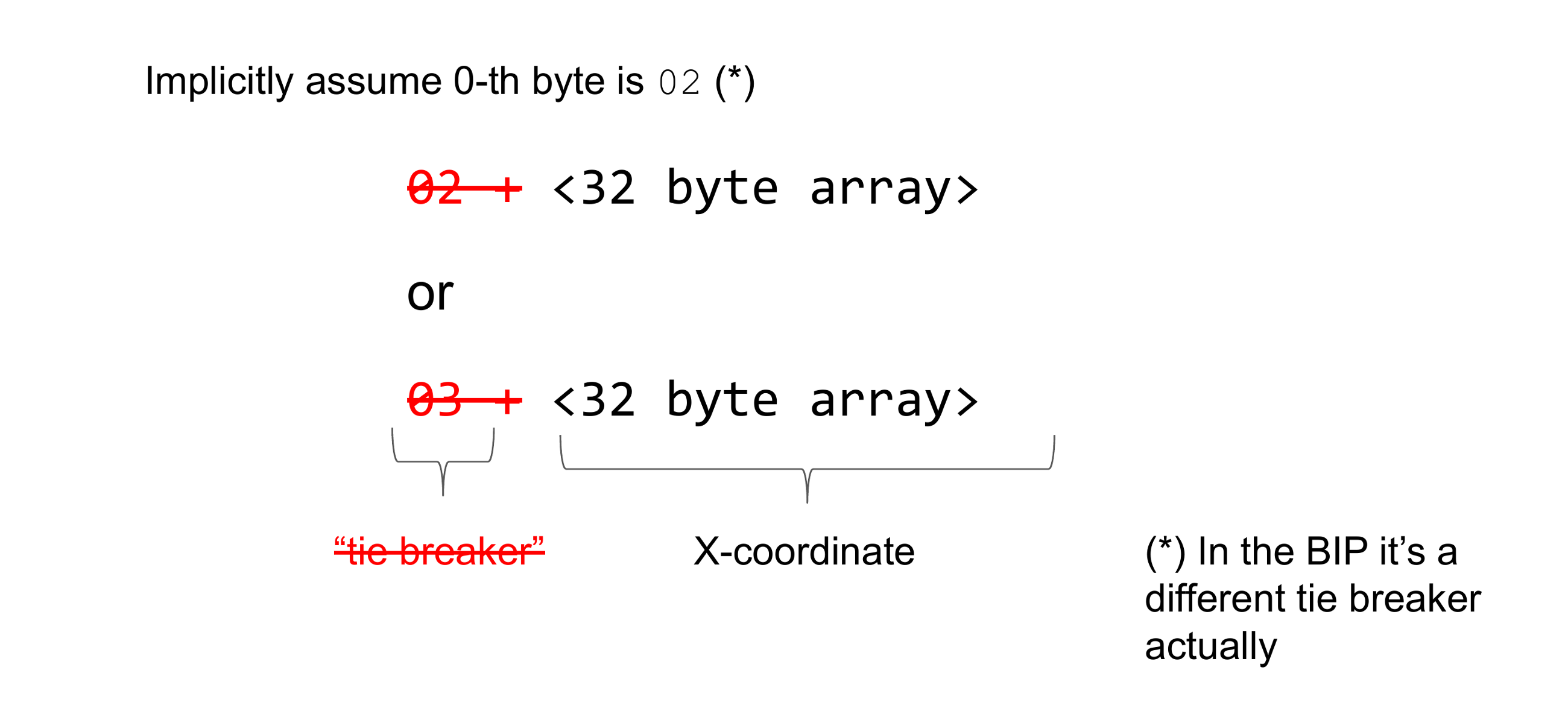
最近，BIP-Schnorr從使用壓縮的public key更改為僅使用x-only public keys。 不同之處在於tie breake不再是public key的一部分。 而是隱式地假設tie breaker為2。 實際上，在BIP中使用了一個不同的tie breaker，但這對於本文而言並不重要。
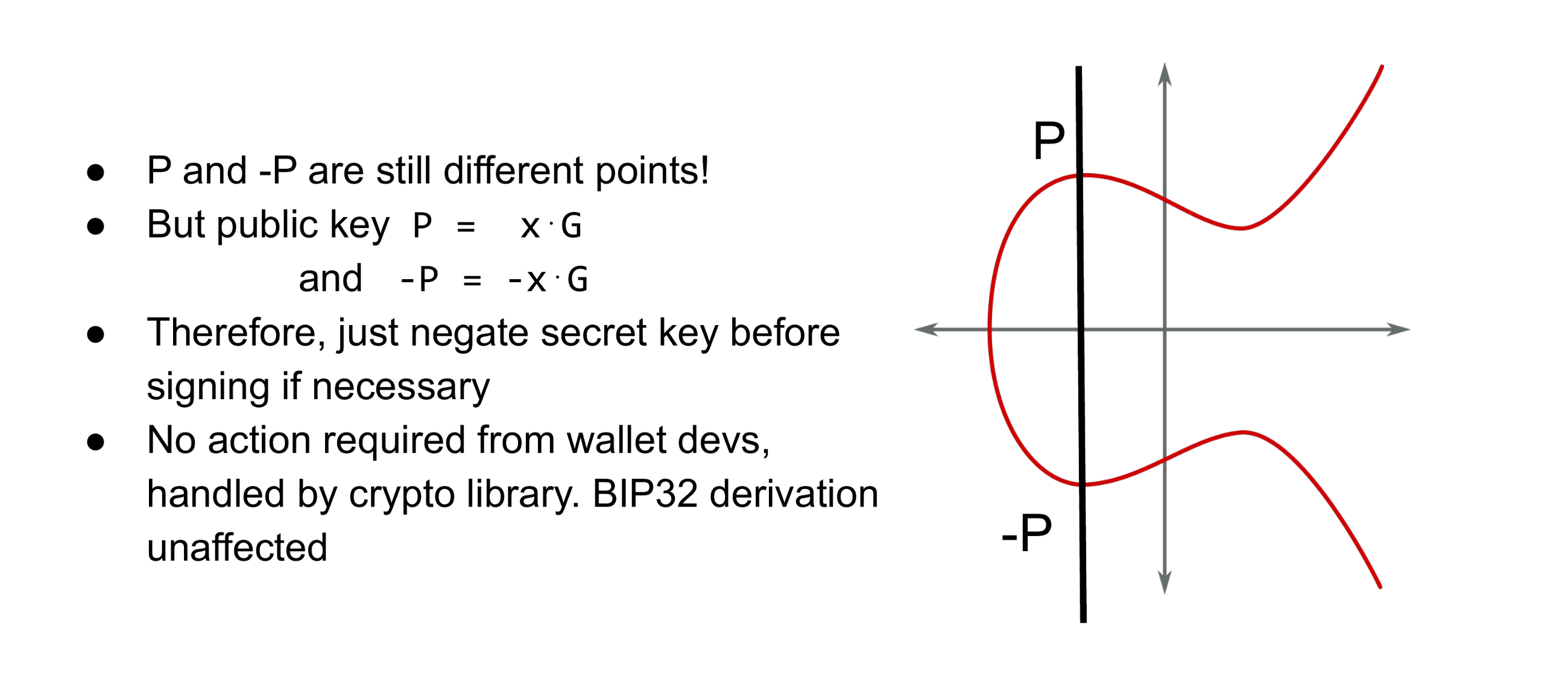
那為什麼行得通呢？ 畢竟，P and -P仍然是不同的點。 由secret key x生成的public key點P是groupG的生成者的x倍。 public key-P的secret key是-x。 答案是我們只需要在正確的時間否定public key和secret key即可。 特別是，簽名演算法會檢查您是否在簽名正確的public key，並在必要時取消secret key。
請務必注意，錢包開發人員無需採取任何措施。 它應該由基礎crypto library處理。 BIP32分層確定性錢包生成也像以前一樣工作，只是您丟棄了第一個byte。
為什麼引入 x-only pubkeys?
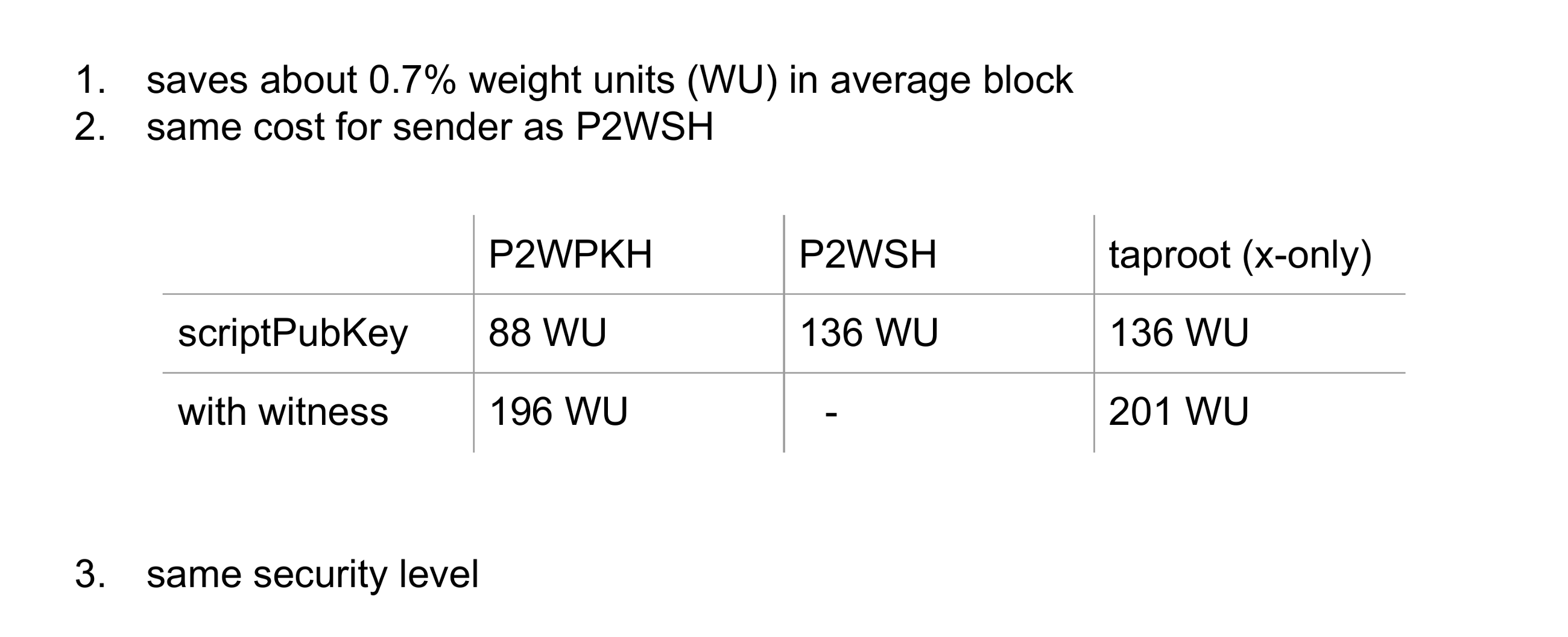
首先，在權重單位方面，scriptPubKey的bytes非常昂貴：x-only 可以在平均完整塊中節省約0.7％的權重單位。 其次，發件人創建scriptPubKey的成本與136個權重單位中的pay-to-witness-script-hash相同。 從理論上講，如果Taproot的價格比舊版隔離見證的價格高，則採用它的速度會更慢。
其次，發起人創建scriptPubKey的成本與pay-to-witness-script-hash”中的136權重單位相同。 從理論上講，如果Taproot的價格比舊的“隔離見證版本”貴，則採用它的速度會更慢。
Pay-to-witness-pub-key-hash scriptPubKey的權重仍遠小於Taprootoutput，因為它們僅包含20-byte hashed public key，但這對於Taproot來說是不安全的。
只是為了完整說明，如果我們考慮take the witness weight into account，Taproot和pay to witness pubkey hash非常相似。
Proof sketch
現在讓我們看一下為什麼這是安全的。
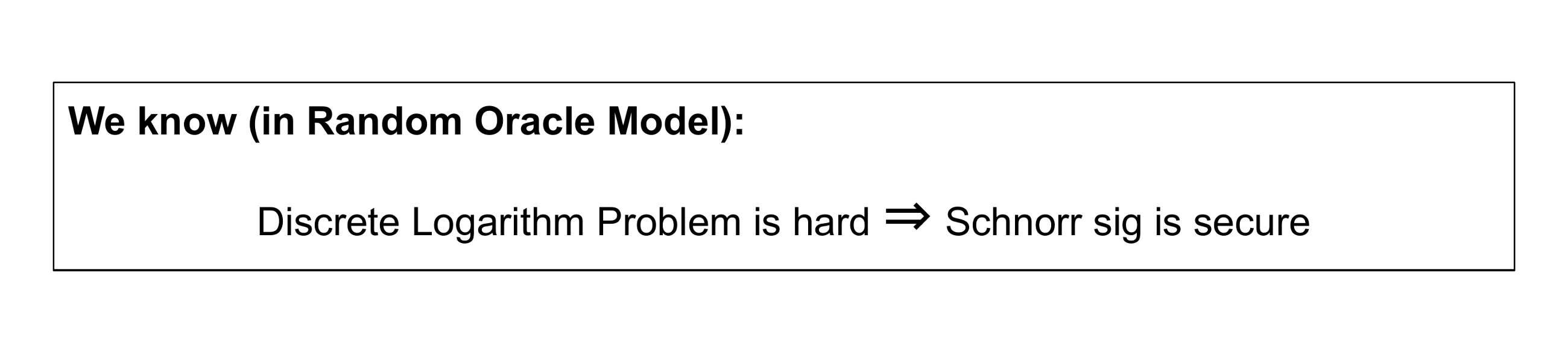
我們知道的是，在隨機預言模型中，如果離散對數問題很困難，那麼Schnorr簽名是安全的。 這意味著在不知道secret key的情況下無法偽造簽名。
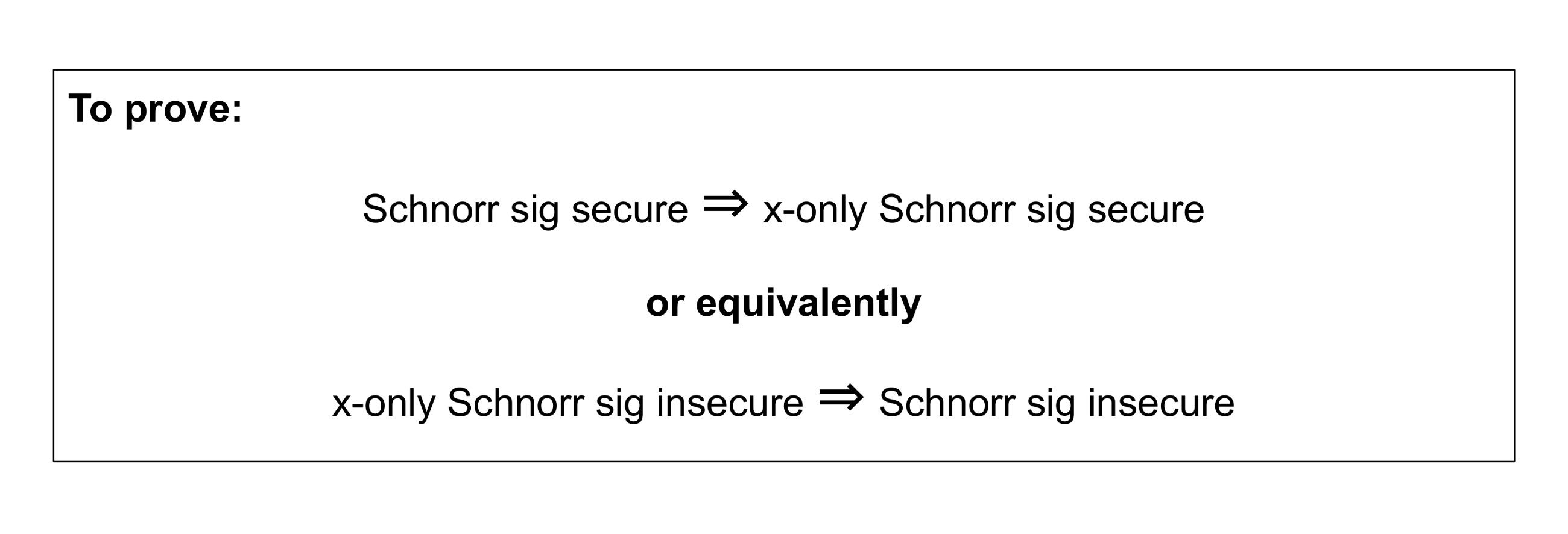
現在我們要證明的是帶有壓縮public key的Schnorr簽名是否安全，那麼x-only的Schnorr簽名是安全的。 或等效地，如果x-only的Schnorr簽名不安全，則Schnorr簽名不安全。
因此，我們假設存在一種偽造Schnorr簽名的演算法，如下圖右圖所示。
Schnorr 簽名是一個元組。 第一個元素是稱為的public nonce，它是通過將secret nonce與group generator相乘而生成的。
第二個元素結合了secret nonce和secret key x。 這裡唯一重要的部分是Schnorr簽名涉及一些hash計算。 我們現在假設的是，在某些時候，偽造者必須計算hash值-沒有其他方法可以產生偽造品。 為了在形式證明(formal proof)中正確定義此值，將hash函數替換為稱為Random Oracle的理想設備。 為了方便說明，我們將繼續稱他為hash function。
現在，我們要做的是構建一種演算法，該演算法響應提供了壓縮public key的挑戰者，並期望獲得Schnorr簽名偽造作為回報。 我們將以某種方式利用x-only的Schnorr簽名偽造者。 這只是一種演算法，如果您願意，我們可以在虛擬機上運行它。 此外，我們可以修補計算hash函數的偽造者程式碼，以返回所需的任何內容。 替換的hash函數必須隨機尋找x-only的Schnorr簽名偽造者，因為否則它可以檢測到它在模擬中並且行為不同。
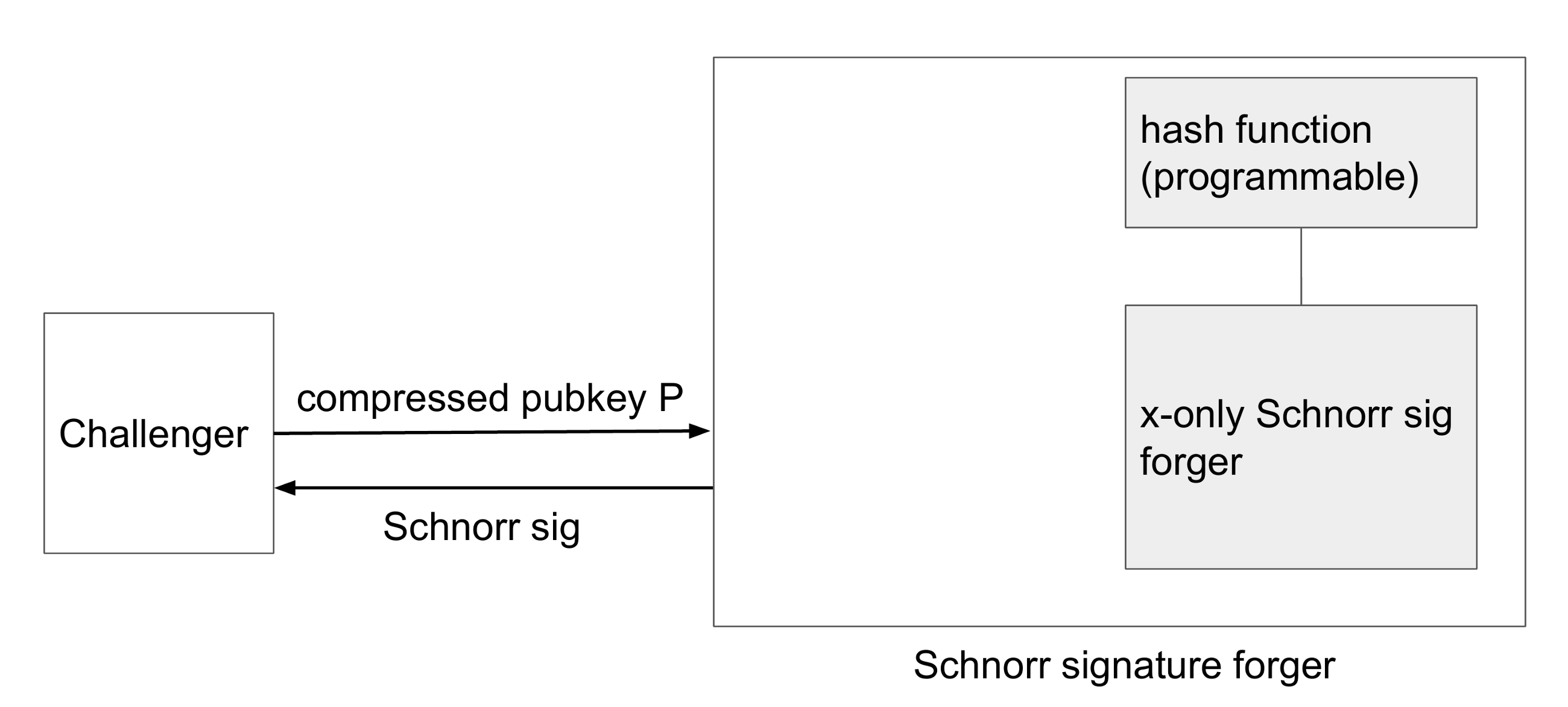
現在，讓我們看一下第一種情況，即public key的第一個byte為2，，這與我們隱含地假定為x-only pubkeys相同。 在這種情況下，我們只需要刪除第一個byte，將其傳遞給偽造者，讓它做事情，然後將Schnorr簽名傳遞給挑戰者即可。
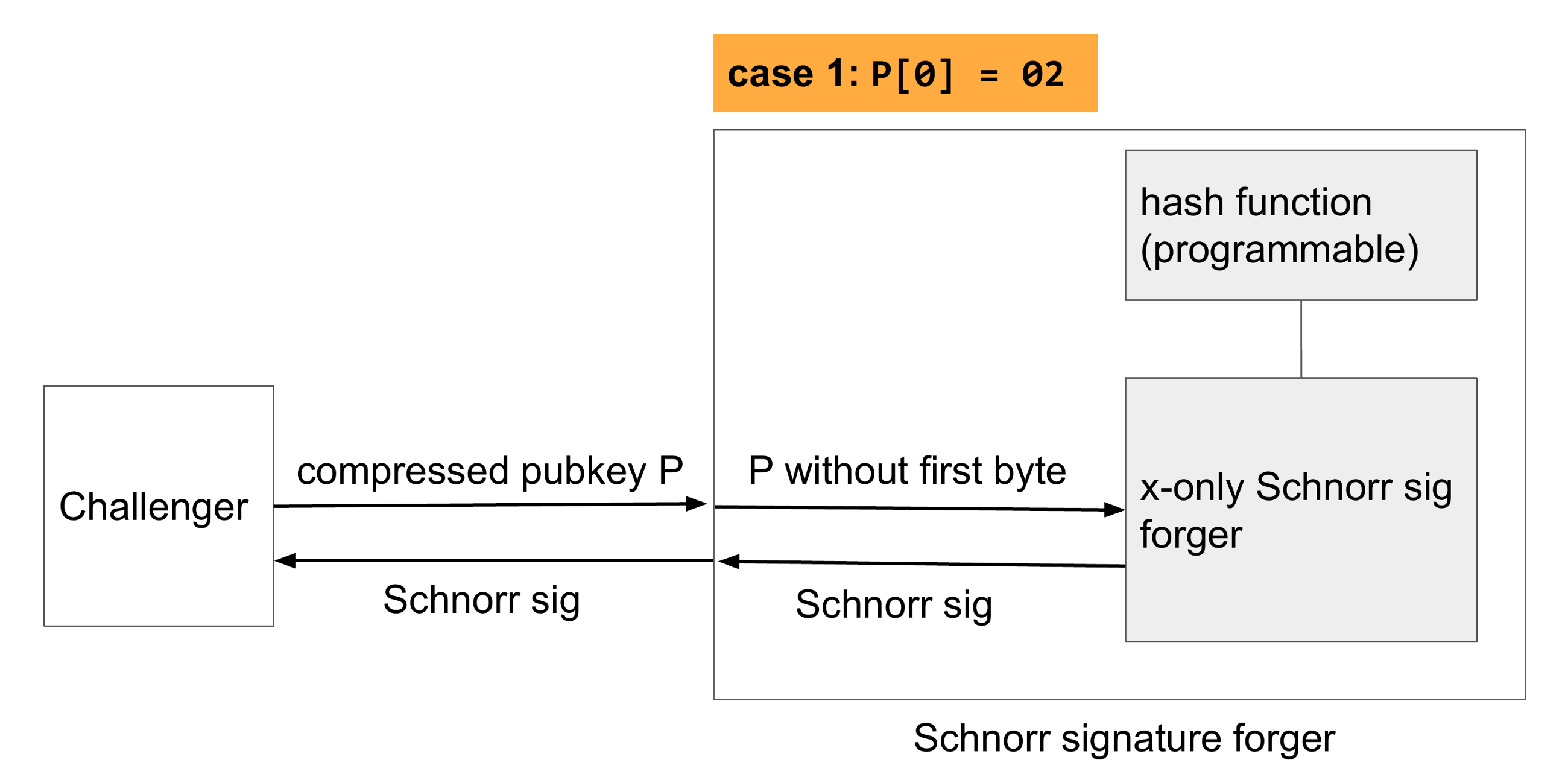
在另一種情況下，第一個byte為3。 同樣，我們將不帶第一個byte的pubkey傳遞給偽造者，但是現在x-only偽造者會將public key解碼為-P，因此將創建的簽名將用於錯誤的public key。 我們通過對hash函數進行編程來解決此問題，以返回挑戰者使用的hash函數output的負數。 然後，我們僅等待偽造者的答复並將其傳遞給挑戰者。
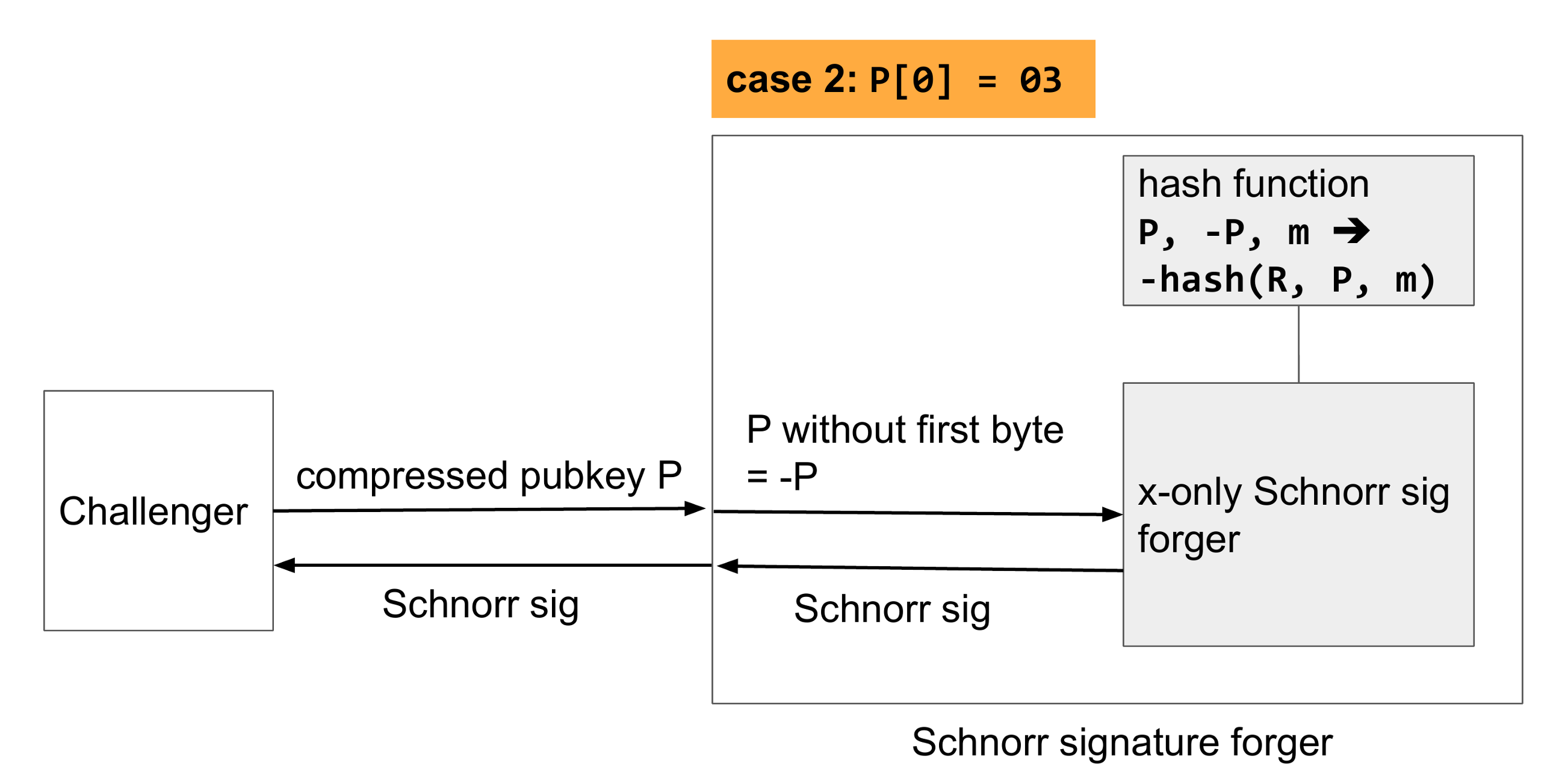
取反的hash值會為該取反的點生成Schnorr簽名，因此挑戰者將很樂意接受該簽名。
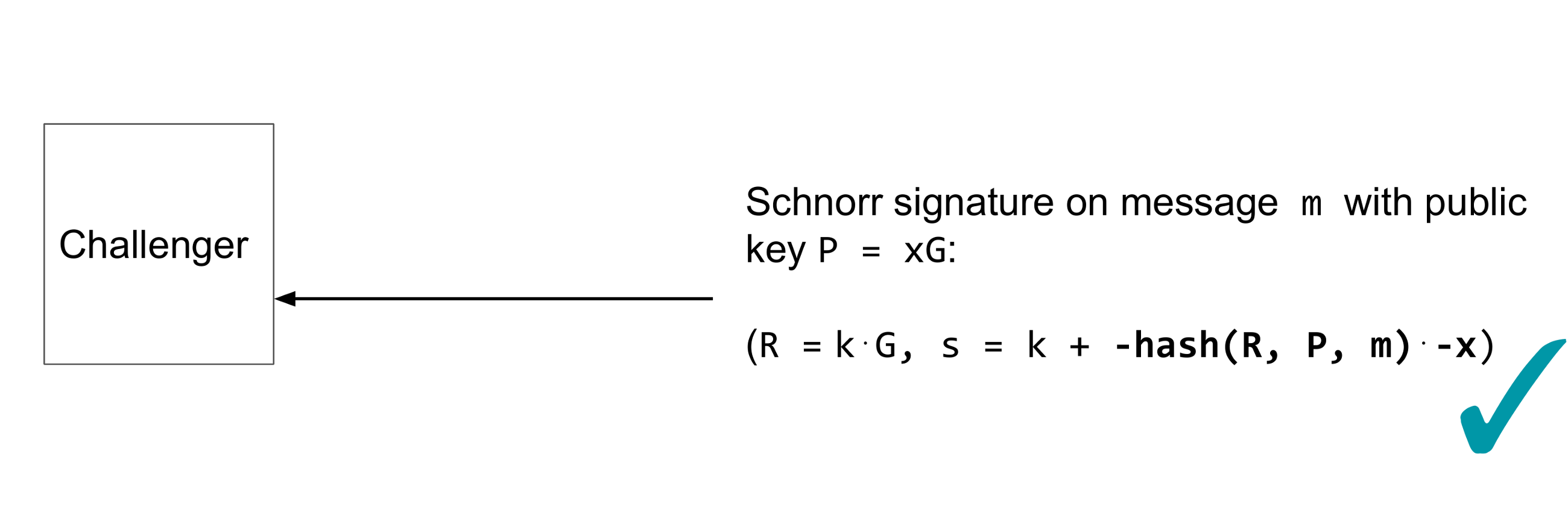
總而言之，我們顯示的是，如果存在x-only Schnorr簽名偽造者，則存在壓縮的pubkey Schnorr簽名偽造者，或者等效地，我們可以假設x-only Schnorr簽名偽造者是安全的。
我們還顯示了一些不直觀的事實，即破壞x-only的難度等於破壞壓縮的public key簽名方案。 簡而言之，tie breaker從來沒有在方案的安全性上添加任何內容。 攻擊者可以根據需要在應用x-only攻擊之前簡單地否定密鑰。 與分組操作（在這種情況下為點加法）相比，當確定攻擊的難度時，該操作通常被計數，否定操作是微不足道的。 在secp256k1的情況下，它只是對場序取模的整數（Y坐標）的取反，接近2²⁵⁶。 在任何現代處理器上，這幾乎不需要時間（在我的筆記本電腦上只需幾納秒），這意味著在硬度上的差異可以忽略不計。
結論 | Conclusion
總結，BIP-schnorr和BIP-taproot最近（2019年9月）進行了調整，以使用32 byte的x-only public keys。 如果在比特幣上採用Schnorr簽名，這將進一步優化已經很低的交易權重。
這種變化的程度相對較低，並且錢包開發人員不必對此太在意。 使用壓縮密鑰可以將x-only Schnorr signatures的安全性降低為Schnorr signatures。
BIP-schnorr和BIP-taproot從草稿狀態到提案狀態正在逐漸成熟。 我們正在尋找反饋，因此可以隨時閱讀，實施BIP或試用BIP-schnorr和BIP-taproot的實施。 Optech Taproot研討會和Taproot評論俱樂部提供的Jupyter筆記本是用於了解有關BIP的很好的資源。
- *BIP-schnorr and BIP-taproot are slowly maturing from the draft status to the proposal status. We’re looking for feedback, so feel free to read the BIPs, implement them, or play with implementations of BIP-schnorr and BIP-taproot. Very good resources for learning more about the BIPs are this Jupyter notebook from the Optech Taproot workshop and the Taproot Review Club.**
