Published: Nov 18, 2019 by Cypherpunks Core
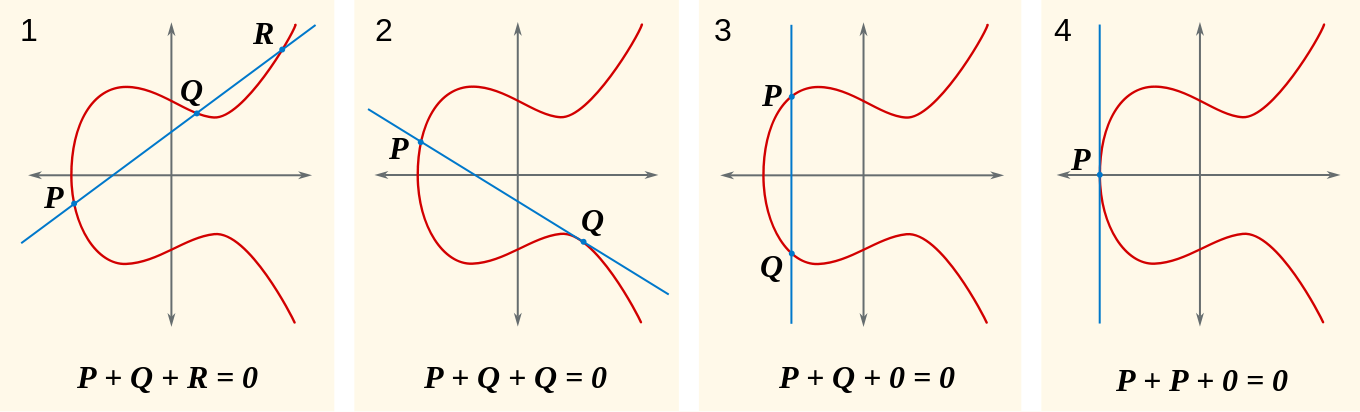
[原文]secp256k1 是指比特幣中使用的 ECDSA 曲線的參數 ，並且在高效密碼學標準（SEC）（Certicom Research，文件）中進行了定義。
在比特幣開始流行之前，secp256k1 幾乎從未使用過，但由於其幾個不錯的屬性，它現在越來越受歡迎。大多數常用曲線具有隨機結構，但 secp256k1 是以特殊的非隨機方式構建的，可以實現特別高效的計算。 因此，如果實施得到充分優化，它通常比其他曲線快 30％ 以上 。 另外，與流行的NIST曲線不同，secp256k1 的常量是以可預測的方式選擇的，這大大降低了曲線建立者在曲線中插入任何後門的可能性。
下面看一下這裡面的函數圖：
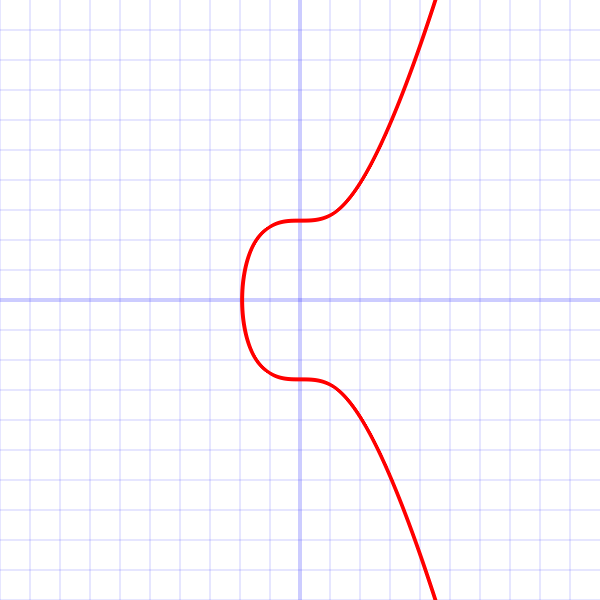
- *Secp256k1 是 secp256k1 橢圓曲線\(y^2 = x^3 + 7\)在實數上的圖形。請注意，因為 secp256k1 實際上是在欄位\(Zp\)上定義的，所以它的圖形實際上看起來像是隨機分散的點，而不是像圖中這樣是連續的點。**
技術細節
從標準摘錄：
與 Koblitz 曲線 secp256k1 相關聯的\(Fp\)上的橢圓曲線域參數由單元\(T=（p，a，b，G，n，h）\)指定，其中有限域\(Fp\)由下式定義：
p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
= 2256 - 232 - 29 - 28 - 27 - 26 - 24 - 1
\(Fp\)上的曲線E：\(y^2 = x^3 + ax + b\)由下式定義：
a = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
b = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007
壓縮形式的基點\(G\)是：
G = 02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
而在未壓縮的形式是：
G = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
最後，\(G\)的迴圈因子\(n\)(就是指\(nG=G\))和輔因子\(h\)如下：
n = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
h = 01
屬性
- secp256k1 具有特徵\(p\)，它的素數域定義為 ℤp。常用的一些其他曲線具有特徵2，並且在二進位制伽羅瓦(Galois)域\(GF(2n)\)上定義，但 secp256k1 不是其中之一。
- 因為一個常數為零，曲線方程中
ax項始終為零，因此曲線方程變為\(y^2 = x^3 + 7\)。
也可以看看
- secp256k1是什麼（ Pieter Wuille 的比特幣堆棧交換答案）
