以太坊有兩種不同類型的帳戶，可以擁有和控制ether：外部擁有帳戶（EOA）和合同。在本節中，我們將研究使用密碼學來確定外部擁有帳戶（即私人密鑰）對ether的所有權。

EOAs中以太的所有權通過 數字密鑰 digital keys，以太坊地址和數位簽章 建立 。數字密鑰實際上並不儲存在區塊鏈中或在以太坊網路上傳輸，而是由用戶創建並儲存在檔案或稱為錢包的簡單資料庫中。用戶錢包中的數字密鑰完全獨立於以太坊協議，可以由用戶的錢包軟體生成和管理，無需參考區塊鏈或訪問互聯網。數字密鑰可實現以太坊的許多有趣特性，包括去中心化的信任和控制以及所有權證明。

以太坊交易需要將有效的數位簽章包含在區塊鏈中，該簽名只能使用密鑰生成；因此，任何擁有該密鑰副本的人都可以控制ether。以太坊交易中的數位簽章證明了資金的真正所有者。

數字密鑰成對組成，密鑰和公鑰。將公鑰視為類似於銀行帳號，私鑰類似於私密PIN，用於控制帳戶。以太坊的用戶很少看到這些數字密鑰。在大多數情況下，它們儲存在錢包檔案內並由以太坊錢包軟體管理。

在以太坊交易的付款部分中，預期收款人由以太坊地址表示，該地址與支票上的收款人名稱相同（即“付款給誰”）。在大多數情況下，以太坊地址是從公鑰生成並對應的。但是，並非所有以太坊地址都代表公鑰。他們也可以代表合同，我們將在 [contracts] 中看到。以太坊地址是用戶常會看到的唯一密鑰表示，因為這是他們需要與世界分享的部分。

首先，我們將介紹密碼學並解釋以太坊使用的數學。接下來，我們將看看密鑰是如何生成，儲存和管理的。最後，我們將回顧用於表示私鑰和公鑰以及地址的各種編碼格式。

公鑰密碼技術是現代資訊安全的核心概念。首先由Martin Hellman，Whitfield Diffie和Ralph Merkle在20世紀70年代公開發明的，這是一個巨大的突破，它激起了公眾對密碼學領域的廣泛興趣。在70年代以前，強大的密碼學知識在政府的控制下，很少有公開的研究，直到公鑰密碼技術研究的公開發表。

公鑰密碼系統使用唯一的密鑰來保護資訊。這些獨特的密鑰基於具有獨特屬性的數學函數：它們很容易在一個方向上計算，但很難在相反方向上計算。基於這些數學函數，密碼學能夠創建數字密鑰和不可偽造的數位簽章，這些簽名由數學定律保證。

例如，計算兩個大質數的乘積是微不足道的。但是給定兩個大質數的乘積，很難找到這兩個質數（稱為素因式分解問題）。假設我提供數字6895601並告訴你它是兩個質數的乘積。找到這兩個質數要比讓它們相乘生產6895601要困難得多。

如果你知道一些祕密資訊，這些數學函數可以很容易地被反轉。在我們上面的例子中，如果我告訴你一個主質數是1931，你可以簡單地用一個簡單的除法找到另一個：6895601/1931 = 3571。這樣的函數被稱為trapdoor函數因為給定一個祕密資訊，你可以採取一個快捷方式，使得反轉該函數很簡單。

在密碼學中有用的另一類數學函數基於橢圓曲線上的算術運算。在橢圓曲線算術中，乘以模數是簡單的，但是除法是不可能的（一個被稱為離散對數的問題）。橢圓曲線密碼術在現代計算機系統中被廣泛使用，並且是以太坊（和其他密碼貨幣）數字密鑰和數位簽章的基礎。

在以太坊，我們使用公鑰加密技術來創建一個密鑰對，以控制對ether的訪問，並允許我們對合同進行身份驗證。密鑰對由私鑰和唯一公鑰組成，並且被認為是“一對兒”，因為公鑰是從私鑰中派生出來的。公鑰用於接收資金，私鑰用於創建數位簽章來簽署交易以支付資金。數位簽章也可用於驗證合同的所有者或用戶，我們將在 << contract_authentication>> 中看到。

公鑰和私鑰之間存在數學關係，允許私鑰用於在消息上生成簽名。該簽名可以在不公開私鑰的情況下使用公鑰進行驗證。

當使用ether時，當前所有者在交易中呈現她的公鑰和簽名（每次不同，但是使用相同的私鑰創建）。通過公鑰和簽名，以太坊系統中的每個人都可以獨立驗證並接受交易的有效性，從而確認在轉移ether的人擁有他們。

私鑰只是一個隨機選取的數字。私有密鑰的所有權和控制權是用戶控制與相應以太坊地址相關聯的所有資金的基礎，也是對該地址的合同的訪問權授權。通過證明交易中使用的資金的所有權，私鑰用於創建花費ether所需的簽名。私鑰在任何時候都必須保密，因為向第三方透露密鑰相當於讓他們控制以太和由該密鑰保證的合同。私鑰還必須備份並防止意外丟失。如果它丟失了，無法恢復，它保護的資金也將永遠丟失。

生成密鑰的第一步也是最重要的一步是找到一個安全的熵源或隨機源。創建以太坊私鑰基本上與“選擇1到2²⁵⁶之間的數字”相同。只要不可預測和不可重複，用於選擇該數字的確切方法並不重要。以太坊軟體使用底層作業系統的隨機數生成器生成256位熵（隨機性）。通常，作業系統隨機數生成器是由一個人為的隨機源進行初始化的，這就是為什麼可能會要求你將鼠標左右搖擺幾秒鐘，或者按下鍵盤上的隨機鍵。

更確切地說，可能的私鑰範圍略小於2²⁵⁶。在以太坊中，私鑰可以是1和n-1之間的任何數字，其中n是定義為使用的橢圓曲線的階數的常數（n = 1.158*10⁷⁷，略小於2²⁵⁶）（參見橢圓曲線密碼學解釋）。為了創建這樣的密鑰，我們隨機選擇一個256位數字並檢查它是否小於n-1。在編程方面，這通常是通過將從密碼學安全的隨機源收集的更大的隨機比特串提供給256位雜湊演算法（如Keccak-256或SHA256）（參見 [cryptographic_hash_algorithm]），產生一個256位數字。如果結果小於n-1，我們有一個合適的私鑰。否則，我們只需再次嘗試使用另一個隨機數。

以下是以十六進制格式顯示的隨機生成的私鑰（k）（256位，顯示為64個十六進制數字，每個4位）：

以太坊公鑰是一個橢圓曲線上的點 point，意思是它是一組滿足橢圓曲線方程的X和Y座標。

簡單來說，以太坊公鑰是兩個數字，並聯在一起。這些數字是通過一次單向的計算從私鑰生成的。這意味著，如果你擁有私鑰，則計算公鑰是微不足道的。但是你不能從公鑰中計算私鑰。

公鑰使用橢圓曲線乘法和私鑰計算，這是不可逆的：K = k * G，其中k是私鑰，G是一個稱為generator point的常數點，K是結果公鑰。如果你知道K，那麼稱為“尋找離散對數”的逆運算就像嘗試所有可能的k值一樣困難，也就是蠻力搜索。

簡單地說：橢圓曲線上的算術不同於“常規”整數算術。點（G）可以乘以整數（k）以產生另一點（K）。但是沒有除法這樣的東西，所以不可能簡單地用公共密鑰K除以點G來計算私鑰k。這是公鑰密碼技術和密碼貨幣中描述的單向數學函數。

在我們演示如何從私鑰生成公鑰之前，我們先來看一下橢圓曲線加密。

橢圓曲線密碼術是一種基於離散對數問題的非對稱或公鑰密碼體系，如橢圓曲線上的加法和乘法運算。

A visualization of an elliptic curve 是橢圓曲線的一個例子，類似於以太坊使用的曲線。

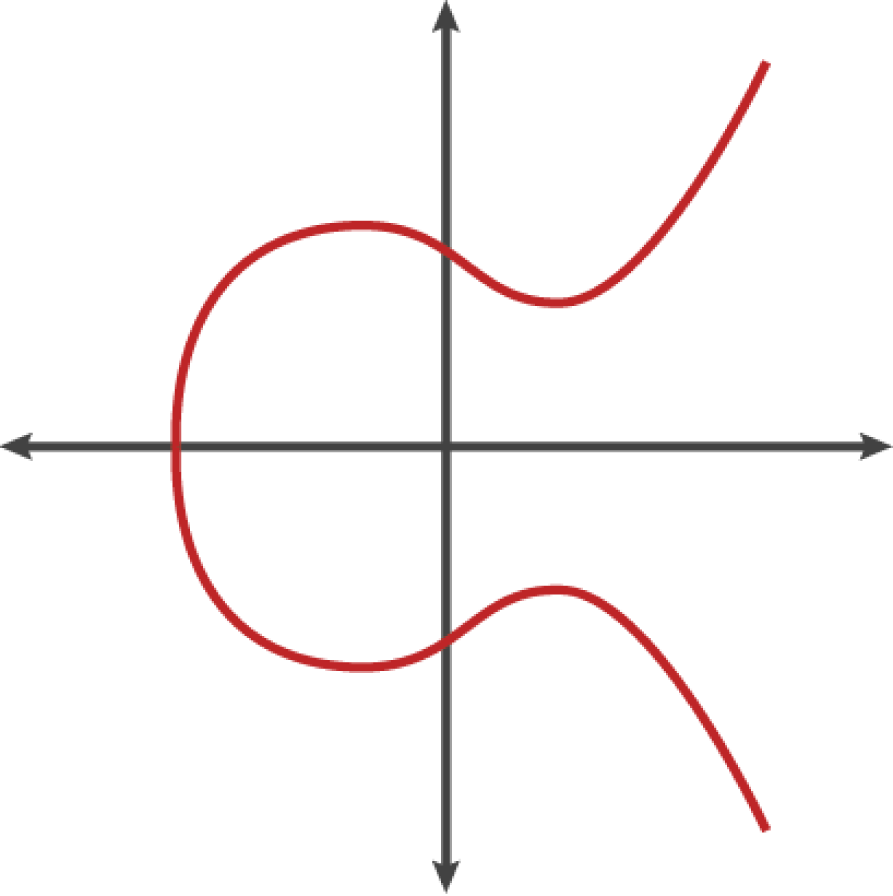
以太坊使用特定的橢圓曲線和一組數學常數，由國家標準與技術研究院（NIST）制定的名為 secp256k1 的標準中所定義的。secp256k1 曲線由以下函數定義，該函數產生一個橢圓曲線：

或

mod p (模質數p) 表示該曲線在質數階p的有限域上，也寫作 \(\( \mathbb{F}_p \)\), 其中 p = 2²⁵⁶ – 2³² – 2⁹ – 2⁸ – 2⁷ – 2⁶ – 2⁴ – 1, 一個非常大的質數。

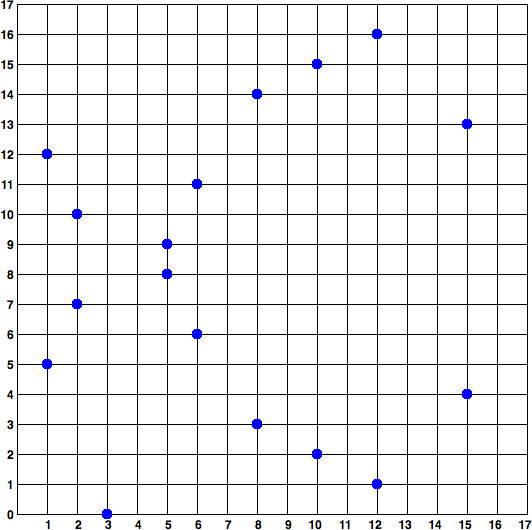
因為這條曲線是在有限的質數階上而不是在實數上定義的，所以它看起來像是一個散佈在二維中的點的模式，使得難以可視化。然而，數學與實數上的橢圓曲線的數學是相同的。作為一個例子，Elliptic curve cryptography: visualizing an elliptic curve over F(p), with p=17 在一個更小的質數階17的有限域上顯示了相同的橢圓曲線，顯示了一個網格上的點的圖案。secp256k1 以太坊橢圓曲線可以被認為是一個更復雜的模式，在一個不可思議的大網格上的點。

例如，以下是座標為（x，y）的點Q，它是 secp256k1 曲線上的一個點：

Using Python to confirm that this point is on the elliptic curve 顯示了如何使用Python檢查它。變數x和y是上述點Q的座標。變數p是橢圓曲線的主要階數（用於所有模運算的質數）。Python的最後一行是橢圓曲線方程（Python中的％運算符是模運算符）。如果x和y確實是橢圓曲線上的點，那麼它們滿足方程，結果為零（0L是零值的長整數）。通過在命令行上鍵入python 並複製下面的每行（不包括提示符 >>>），親自嘗試一下：

很多橢圓曲線數學看起來很像我們在學校學到的整數算術。具體而言，我們可以定義一個加法運算符，而不是添加數字就是在曲線上添加點。一旦我們有了加法運算符，我們也可以定義一個點和一個整數的乘法，等於重複加法。

A lot of elliptic curve math looks and works very much like the integer arithmetic we learned at school. Specifically, we can define an addition operator, which instead of adding numbers is adding points on the curve. Once we have the addition operator, we can also define multiplication of a point and a whole number, such that it is equivalent to repeated addition.

加法定義為給定橢圓曲線上的兩個點 P₁ and P₂ , 第三個點 P₃ = P₁ + P₂, 也在橢圓曲線上。

在幾何上，這個第三點 P₃ 是通過在 P₁ 和 P₂ 之間畫一條直線來計算的。這條線將在另外一個地方與橢圓曲線相交。稱此點為 P₃' = (x, y)。然後在x軸上反射得到 P₃ = (x, –y)。

在橢圓曲線數學中，有一個叫做“無窮點”的點，它大致對應於零點的作用。在計算機上，它有時用 x = y = 0表示（它不滿足橢圓曲線方程，但它是一個容易區分的情況，可以檢查）。有幾個特殊情況解釋了“無窮點”的需要。

如果 P₁ 和 P₂ 是同一點，P₁ and P₂ 之間的直線應該延伸到曲線上 P₁ 的切線。 該切線恰好與曲線在一個新點相交。你可以使用微積分技術來確定切線的斜率。我們將我們的興趣侷限在具有兩個整數座標的曲線上，這些技巧令人好奇地工作！

在某些情況下（即，如果 P₁ 和 P₂ 具有相同的x值但不同的y值），切線將精確地垂直，在這種情況下P3 =“無窮點”。

如果 P₁ 是“無窮點”，那麼 P₁ + P₂ = P₂。 類似地, 如果 P₂ 是“無窮點”，P₁ + P₂ = P₁。這顯示了無窮點如何扮演零在“正常”算術中扮演的角色。

+ 是可結合的, (A + B) + C = A + (B + C). 這表示 A + B + C 不加括號也沒有歧義。

現在我們已經定義了加法，我們可以用擴展加法的標準方式來定義乘法。對於橢圓曲線上的點P，如果k是整數，則 k * P = P + P + P + …​ + P (k 次)。請注意，在這種情況下，k有時會被混淆地稱為“指數”。

以一個隨機生成的數字k的私鑰開始，我們通過將它乘以稱為generator point G的曲線上的預定點，在曲線上的其他位置產生另一個點，這是相應的公鑰K。生成點被指定為secp256k1標準的一部分，對於secp256k1的所有實現始終相同，並且從該曲線派生的所有密鑰都使用相同的點G：

其中k是私鑰，G是生成點，K是生成的公鑰，即曲線上的一個點。因為所有以太坊用戶的生成點始終相同，所以G乘以G的私鑰總是會導致相同的公鑰K。k和K之間的關係是固定的，但只能從k到K的一個方向進行計算。這就是為什麼以太坊地址（來自K）可以與任何人共享，並且不會洩露用戶的私鑰（k）。

正如我們在 橢圓曲線算術運算中所描述的那樣，k * G的乘法相當於重複加，G + G + G + …​ + G ，重複k次。總而言之，為了從私鑰k生成公鑰K，我們將生成點G添加到自己k次。

讓我們應用這個計算來找到我們在 私鑰 中給出的特定私鑰的公鑰：

密碼庫可以幫助我們使用橢圓曲線乘法計算K值。得到的公鑰K被定義為一個點 K = (x,y) ：

在以太坊中，你可以看到公鑰以66個十六進制字符（33字節）的十六進制序列表示。這是從行業聯盟標準高效密碼組（SECG）提出的標準序列化格式採用的，在http://www.secg.org/sec1-v2.pdf[Standards for Efficient Cryptography（SEC1）]中有記載。該標準定義了四個可用於識別橢圓曲線上點的可能前綴：

以太坊只使用未壓縮的公鑰，因此唯一相關的前綴是（十六進制）04。順序連接公鑰的X和Y座標：

因此，我們在 Example public key calculated from the example private key 中計算的公鑰被序列化為：

密碼貨幣相關項目中使用了secp256k1橢圓曲線的幾個實現：

加密雜湊函數在整個以太坊使用。事實上，雜湊函數幾乎在所有密碼系統中都有廣泛應用，這是密碼學家布魯斯•施奈爾（Bruce Schneier）所說的一個事實，他說：“單向雜湊函數遠不止於加密演算法，而是現代密碼學的主要工具。

在本節中，我們將討論雜湊函數，瞭解它們的基本屬性以及這些屬性如何使它們在現代密碼學的很多領域如此有用。我們在這裡討論雜湊函數，因為它們是將以太坊公鑰轉換成地址的一部分。

簡而言之，“雜湊函數是可用於將任意大小的數據映射到固定大小的數據的函數。” Source：Wikipedia。雜湊函數的輸入稱為 原象 _ pre-image_ 或 消息 message。輸出被稱為 雜湊 hash或 摘要 digest。雜湊函數的一個特殊子類別是 加密雜湊函數，它具有對密碼學有用的特定屬性。

加密雜湊函數是一種單向雜湊函數，它將任意大小的數據映射到固定大小的位串，如果知道輸出，計算上不可能重新創建輸入。確定輸入的唯一方法是對所有可能的輸入進行蠻力搜索，檢查匹配輸出。

加密雜湊函數有五個主要屬性 (Source: Wikipedia/Cryptographic Hash Function):

碰撞保護對於防止以太坊中的數位簽章偽造至關重要。

這些屬性的組合使加密雜湊函數可用於廣泛的安全應用程式，包括：

通過研究系統的各個層面，我們會在以太坊找到它的很多應用。

以太坊在許多地方使用Keccak-256加密雜湊函數。Keccak-256被設計為於2007年舉行的SHA-3密碼雜湊函數競賽的候選者。Keccak是獲勝的演算法，在2015年被標準化為 FIPS（聯邦資訊處理標準）202。

然而，在以太坊開發期間，NIST標準化工作正在完成。在標準過程完成後，NIST調整了Keccak的一些參數，據稱可以提高效率。這與英雄告密者愛德華斯諾登透露的檔案暗示NIST可能受到國家安全局的不當影響同時發生，故意削弱Dual_EC_DRBG隨機數生成器標準，有效地在標準隨機數生成器中放置一個後門。這場爭論的結果是對所提議修改的反對以及SHA-3標準化的嚴重拖延。當時，以太坊基金會決定實施最初的Keccak演算法。

由於Ethereum中使用的雜湊函數（Keccak-256）與最終標準（FIP-202 SHA-3）之間的差異造成了混淆，因此正在努力將程式碼中所有的 sha3 的所有實例，操作碼和庫重新命名為 keccak256。詳情請參閱https://github.com/ethereum/EIPs/issues/59[ERC-59]。

如何判斷你使用的軟體庫是FIPS-202 SHA-3還是Keccak-256（如果兩者都可能被稱為“SHA3”）？

一個簡單的方法是使用test vector，一個給定輸入的預期輸出。最常用於雜湊函數的測試是empty input。如果你使用空字串作為輸入運行雜湊函數，你應該看到以下結果：

因此，無論調用什麼函數，都可以通過運行上面的簡單測試來測試它是否是原始的Keccak-256或最終的NIST標準FIPS-202 SHA-3。請記住，以太坊使用Keccak-256，儘管它在程式碼中通常被稱為SHA-3。

接下來，讓我們來看一下Ethereum中Keccak-256的第一個應用，即從公鑰生成以太坊地址。

以太坊地址是 唯一識別碼 unique identifiers，它們是使用單向雜湊函數（Keccak-256）從公鑰或合約派生的。

在我們之前的例子中，我們從一個私鑰開始，並使用橢圓曲線乘法來派生一個公鑰：

Private Key k:

Public Key K (X and Y coordinates concatenated and shown as hex):

我們使用Keccak-256來計算這個公鑰的hash：

然後我們只保留最後的20個字節（大端序中的最低有效字節），這是我們的以太坊地址：

大多數情況下，你會看到帶有前綴“0x”的以太坊地址，表明它是十六進制編碼，如下所示：

以太坊地址是十六進制數字，從公鑰的Keccak-256雜湊的最後20個字節匯出的識別碼。

與在所有客戶端的用戶界面中編碼的比特幣地址不同，它們包含內建校驗和來防止輸入錯誤的地址，以太坊地址以原始十六進制形式呈現，沒有任何校驗和。

該決定背後的基本原理是，以太坊地址最終會隱藏在系統高層的抽象（如名稱服務）之後，並且必要時應在較高層添加校驗和。

回想起來，這種設計選擇導致了一些問題，包括由於輸入錯誤地址和輸入驗證錯誤而導致的資金損失。以太坊名稱服務的開發速度低於最初的預期，諸如ICAP之類的替代編碼被錢包開發商採用得非常緩慢。